AP微积分核心考点:洛必达法则

　　新东方在线AP频道为大家带来AP微积分核心考点:洛必达法则一文，希望对大家AP备考有所帮助。更多精彩尽请关注新东方在线AP频道!

　　AP微积分之洛必达法则——杭晓渝

　　大家好，今天我们来讨论一下AP微积分里面求函数极限的一个极为方便的工具——洛必达法则。求极限、求导数、求积分是微积分的三大基本功，可以说，掌握洛必达法则是我们理解微积分函数极限的一块必不可少的奠基石。那么，什么是洛必达法则?它又是怎样帮助我们求极限的呢?让我们先来考虑几个简单的例子：

　　例1：

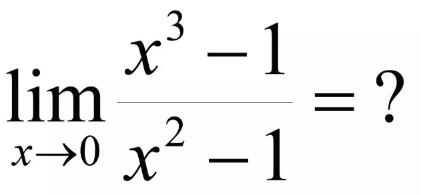
　　利用极限的四则运算法则，把 X=1 分别带入分子、分母里面，得到的结果：

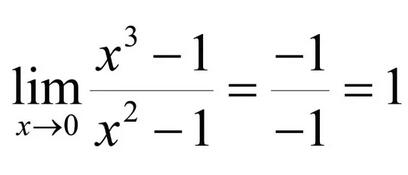
　　例2：

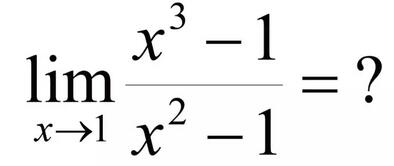
　　啊哈!这和上个例子几乎一样，我们能不能依葫芦画瓢呢?把 X=1 代入分子、分母，得到：

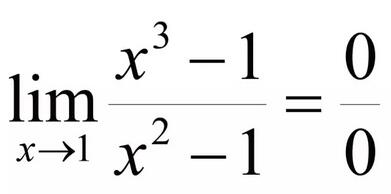
　　,这不是没有意义么?

　　例3：

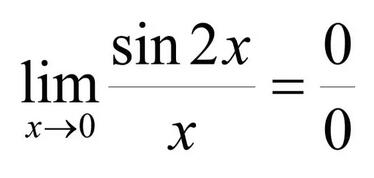
　　例4：

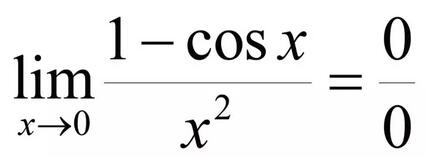
　　大家可以看到，后三种极限就不能应用极限的四则运算法则直接代入了。因为代入之后得到的表达式是一个未确定的形式，所以，这类极限通常被叫做“未定式”，可以简单地记作

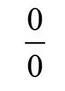
　　型。但是，未定并不表示这些极限是不存在的。微积分学到这个时候，我们手里对付这类问题的工具也有几个了，有时要通过消除零因子(约分)来求极限，像例2：

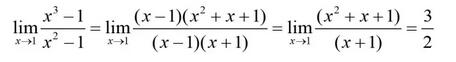
　　有时要用已知结果求极限，像例3，由于

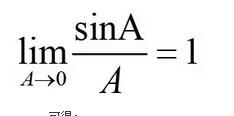
　　，可得：

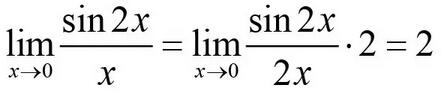
　　有时更要结合用三家函数的恒等变换来求极限，像例4：

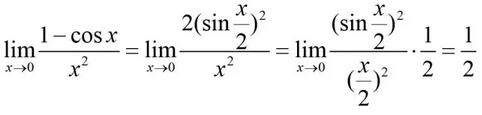
　　这些方法尽管有效，但在应用的时候必须针对具体问题进行具体分析，要求一定的技巧和灵活性。像是一个杂牌军，东一榔头、西一棒子。相比之下，我们下面将要介绍的洛必达法则是一个比较全面系统的过程，应用起来直接、方便，算是正规军正面进攻的武器。

　　让我们再重新计算一下例2：

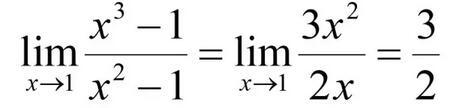
　　细心的同学可能已经发现，我把原函数分式上下同时求导，从而绕开了

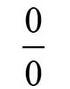
　　型“未定式”这样一个绊脚石。下一个问题自然是，你为什么可以这样对分子、分母同时求导还能保证极限不变呢?

法则的形式十分简单：在

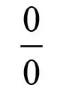
　　的情形下，函数商的极限等于导数商的极限。换句话说，求未定式极限的时候，可以通过分子、分母同时求导的方式来转化原来的表达式，继续求极限。这就是洛必达法则的精髓所在。

　　下面咱们尝试着用洛必达法则来计算一下前面的几个例子。

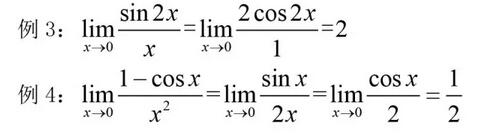
　　在上面的计算过程中，大家可以看到，只要是未定式，我们就可以使用洛必达法则对分子分母同时求导。一次应用之后，如果还是未定式，可以反复使用法则。直到所求极限形式已经不是未定式，就可以直接求极限了。

　　洛必达法则的严格证明要利用柯西中值定理，这并不是我们学习AP微积分必须掌握的。但从直观的角度，大家动脑筋思考一下就会意识到它其实就是反映了微积分的基本准则“以直代曲”。回顾例2：

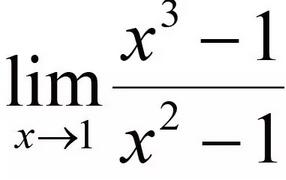
，我们先来看看这两个函数的图像，

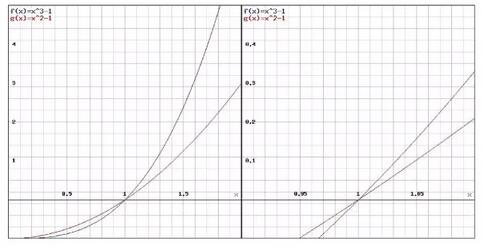
　　这是两根曲线，但由于我们是求在 X=1 附近的极限，可以把图像放大，聚焦在 X=1 附近，就得到了右边的图形。大家可以看到，在小的范围里，这两根曲线就几乎是直线了。这两根直线就是我们学习过的函数在 X=1 的切线，切线方程是

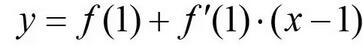
，因此，注意分子分母在 X=1 的函数值都是 0 ，以直代曲，我们可以得到：

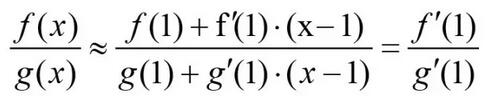
　　这就是洛必达法则啦!

　　以上就是新东方在线AP频道为你带来的AP微积分核心考点:洛必达法则，更多精彩敬请关注新东方在线AP频道。