题目详解
题目来源来自网络
题目来源:
OG详解-OG1 数学2 Q25
正确答案:B
问题反馈收藏题目
详解
Choice B is correct. Since the model estimates that the number of squirrels in the population increased by a fixed percentage, 150%, each year, the model can be represented by an exponential equation of the form 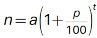 , where a is the estimated number of squirrels in the population at the end of 2015, and the model estimates that at the end of each year, the number is p% more than the number at the end of the previous year. Since the model estimates that at the end of each year, the number was 150% more than the number at the end of the previous year, p = 150. Substituting 150 for p in the equation
, where a is the estimated number of squirrels in the population at the end of 2015, and the model estimates that at the end of each year, the number is p% more than the number at the end of the previous year. Since the model estimates that at the end of each year, the number was 150% more than the number at the end of the previous year, p = 150. Substituting 150 for p in the equation 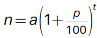 yields
yields 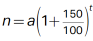 , which is equivalent to n = a (1+1.5)t. or n = a(2.5)t. It’s given that estimated number of squirrels at the end of 2016 was 180. This means that when t = 1, n = 180. Substituting 1 for t and 180 for n in the equation n = a(2.5)t yields 180 = a (2.5)1, or 180 = 2.5a. Dividing each side of this equation by 2.5 yields 72 = a. Substituting 72 for a in the equation n = a (2.5)t yields n = 72 (2.5)t.
, which is equivalent to n = a (1+1.5)t. or n = a(2.5)t. It’s given that estimated number of squirrels at the end of 2016 was 180. This means that when t = 1, n = 180. Substituting 1 for t and 180 for n in the equation n = a(2.5)t yields 180 = a (2.5)1, or 180 = 2.5a. Dividing each side of this equation by 2.5 yields 72 = a. Substituting 72 for a in the equation n = a (2.5)t yields n = 72 (2.5)t.
Choice A is incorrect. This equation represents a model where at the end of each year, the estimated number of squirrels was 150% of, not 150% more than, the
estimated number at the end of the previous year. Choice C is incorrect. This equation represents a model where at the end of each year, the estimated number of squirrels was 150% of, not 150% more than, the estimated number at the end of the previous year, and the estimated number of squirrels at the end of 2015, not the end of 2016, was 180. Choice D is incorrect.This equation represents a model where the estimated number of squirrels at the end of 2015, not the end of 2016, was 180.
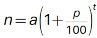 , where a is the estimated number of squirrels in the population at the end of 2015, and the model estimates that at the end of each year, the number is p% more than the number at the end of the previous year. Since the model estimates that at the end of each year, the number was 150% more than the number at the end of the previous year, p = 150. Substituting 150 for p in the equation
, where a is the estimated number of squirrels in the population at the end of 2015, and the model estimates that at the end of each year, the number is p% more than the number at the end of the previous year. Since the model estimates that at the end of each year, the number was 150% more than the number at the end of the previous year, p = 150. Substituting 150 for p in the equation 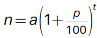 yields
yields 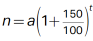 , which is equivalent to n = a (1+1.5)t. or n = a(2.5)t. It’s given that estimated number of squirrels at the end of 2016 was 180. This means that when t = 1, n = 180. Substituting 1 for t and 180 for n in the equation n = a(2.5)t yields 180 = a (2.5)1, or 180 = 2.5a. Dividing each side of this equation by 2.5 yields 72 = a. Substituting 72 for a in the equation n = a (2.5)t yields n = 72 (2.5)t.
, which is equivalent to n = a (1+1.5)t. or n = a(2.5)t. It’s given that estimated number of squirrels at the end of 2016 was 180. This means that when t = 1, n = 180. Substituting 1 for t and 180 for n in the equation n = a(2.5)t yields 180 = a (2.5)1, or 180 = 2.5a. Dividing each side of this equation by 2.5 yields 72 = a. Substituting 72 for a in the equation n = a (2.5)t yields n = 72 (2.5)t.Choice A is incorrect. This equation represents a model where at the end of each year, the estimated number of squirrels was 150% of, not 150% more than, the
estimated number at the end of the previous year. Choice C is incorrect. This equation represents a model where at the end of each year, the estimated number of squirrels was 150% of, not 150% more than, the estimated number at the end of the previous year, and the estimated number of squirrels at the end of 2015, not the end of 2016, was 180. Choice D is incorrect.This equation represents a model where the estimated number of squirrels at the end of 2015, not the end of 2016, was 180.
0
题目标记:
答对了
答错了
漏选了




