题目详解
题目来源来自网络
题目来源:
OG详解-OG1 数学2 Q26
正确答案:B
问题反馈收藏题目
详解
Choice B is correct. Two lines are perpendicular if their slopes are negative reciprocals,meaning that the slope of the first line is equal to -1 divided by the slope of the second line. Each equation in the given pair of equations can be written in slope-intercept form, y = mx + b, where m is the slope of the graph of the equation in the xy-plane and (0,b) is they-intercept. For the first equation, 5x +7y = 1, subtracting 5x from both sides gives 7y =-5x +1, and dividing both sides of this equation by 7 gives y = -57x +17. Therefore, the slope of the graph of this equation is -57. For the second equation, ax + by = 1, subtracting ax from both sides gives by =-ax +1, and dividing both sides of this equation by b gives y = -abx + 1b. Therefore, the slope of the graph of this equation is -ab. Since the graph of the given pair of equations is a pair of perpendicular lines, the slope of the graph of the second equation, -ab, must be the negative reciprocal of the slope of the graph of the first equation, -57. The negative reciprocal of -57is −1(−57) or 75 . Therefore,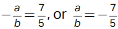 . Similarly,rewriting the equations in choice B in slope-intercept form yields
. Similarly,rewriting the equations in choice B in slope-intercept form yields  . It follows that the slope of the graph of the first equation in choice B is -a2b . Since ab = - 75 ,-a2b is equal to
. It follows that the slope of the graph of the first equation in choice B is -a2b . Since ab = - 75 ,-a2b is equal to 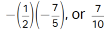 . Since 710 is the negative reciprocal of -107 , the pair of equations in choice B represents a pair of perpendicular lines.
. Since 710 is the negative reciprocal of -107 , the pair of equations in choice B represents a pair of perpendicular lines.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
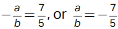 . Similarly,rewriting the equations in choice B in slope-intercept form yields
. Similarly,rewriting the equations in choice B in slope-intercept form yields  . It follows that the slope of the graph of the first equation in choice B is -a2b . Since ab = - 75 ,-a2b is equal to
. It follows that the slope of the graph of the first equation in choice B is -a2b . Since ab = - 75 ,-a2b is equal to 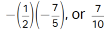 . Since 710 is the negative reciprocal of -107 , the pair of equations in choice B represents a pair of perpendicular lines.
. Since 710 is the negative reciprocal of -107 , the pair of equations in choice B represents a pair of perpendicular lines.Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
0
题目标记:
答对了
答错了
漏选了




